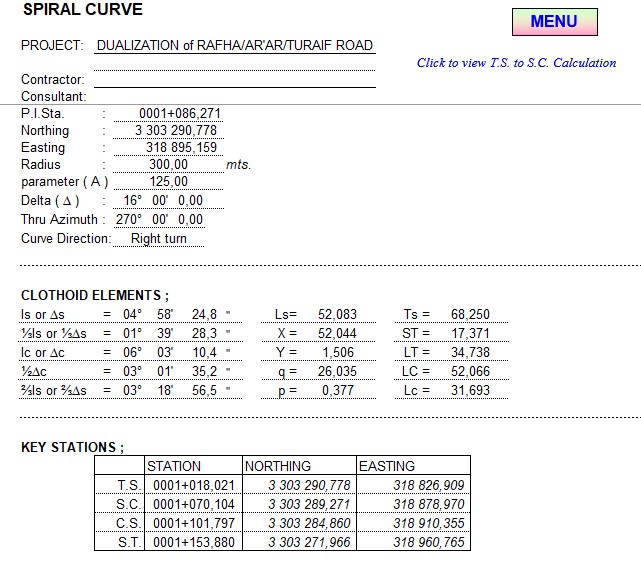
Road Spiral Curve (Clothoid Calculation) Spreadsheet

When it comes to road engineering, the road spiral curve, also known as a clothoid curve, plays a vital role in creating smooth and safe transitions between straight paths and curved sections. This fascinating geometric design not only improves road safety but also enhances the driving experience. In this article, we’ll dive deep into what a spiral curve is, how it works, and why it is indispensable in modern road design.

What Is a Road Spiral Curve?

A spiral curve is a transitional curve used in road and railway alignments to gradually change the curvature between a straight section and a circular curve. This gradual change helps vehicles maintain stability and comfort by reducing sudden shifts in direction.

The spiral curve is often based on the clothoid spiral, a mathematical curve where the radius of curvature decreases or increases uniformly. This unique property ensures a smooth and predictable transition, making it easier for drivers to navigate.

Why Are Spiral Curves Important?

1. Safety: Abrupt changes in direction can cause vehicles to skid or lose control. Spiral curves minimize these risks by allowing drivers to adjust gradually.
2. Comfort: Sudden turns can be jarring for passengers. Spiral curves provide a seamless transition, enhancing the driving experience.
3. Design Efficiency: Engineers can optimize space while adhering to safety and comfort standards, especially on highways and mountainous roads.

Applications of Spiral Curves in Road Design

Spiral curves are used in various road engineering projects, including:

• Highways and Expressways: For smooth entry and exit ramps.
• Mountain Roads: To navigate steep and winding terrains safely.
• Urban Intersections: For roundabouts and merging lanes.

How Spiral Curves Are Designed

The design of a spiral curve involves complex mathematical calculations to determine the length, radius, and alignment. Key factors include:

• Design Speed: Higher speeds require longer spiral curves.
• Radius of Circular Curve: Smaller radii need smoother transitions.
• Terrain and Space Constraints: Spiral curves must adapt to the environment while maintaining safety standards.

Benefits of Spiral Curves in Modern Infrastructure

1. Enhanced Traffic Flow: Vehicles can navigate smoothly, reducing bottlenecks.
2. Reduced Maintenance Costs: Smooth transitions decrease wear and tear on road surfaces.
3. Environmental Impact: Efficient designs minimize land use and ecological disruption.

Challenges in Implementing Spiral Curves

Despite their advantages, spiral curves come with challenges:

• Complex Calculations: Designing spiral curves requires advanced mathematical and engineering skills.
• Cost: The precise construction and surveying involved can increase initial costs.
• Space Requirements: In urban areas, limited space may restrict the use of ideal spiral curves.

Future Trends in Spiral Curve Design

With advancements in technology, engineers now use sophisticated software to design spiral curves with greater precision. Additionally, the integration of autonomous vehicles may demand even more precise alignments, making spiral curves essential for smart road systems.

Conclusion

The road spiral curve is a cornerstone of modern road design, ensuring safety, comfort, and efficiency. Its role in facilitating smooth transitions between straight and curved paths makes it indispensable in the construction of highways, urban roads, and mountain routes. As technology evolves, so too will the methods for designing and implementing these critical road features, paving the way for safer and more efficient transportation systems.

By understanding the importance of spiral curves, we can appreciate the ingenuity behind the roads we travel on every day. Whether you’re an engineer, a student, or simply curious about road design, the spiral curve stands as a testament to how mathematics and engineering come together to shape our world.

Download Link